불확실성, 변동성 그리고 분산
이 글을 목표는 확률의 본질에 대해서 불확실성, 변동석, 분산의 개념으로 설명하려고 한다. 위 개념에 대해서, 대학교 통계학 수업을 들었을때 깊은 고민을 많이 했으며, 그 당시 정리된 생각을 녹여내어 글을 작성했다.
1. 불확실성이란?
내가 똑같은 수행을 하더라도 통제할 수 없는 어떠한 변인 때문에 계속 다른 결과가 나오게 하는 주요 원인이다.
(확률이 존재할 수 있게 하는 근본적인 원인이라 볼 수 있다)
예를 들어, 내가 종이 비행기를 똑같은 힘으로 똑같은 방향으로 10번 수행했다. 과연 그 종이 비행기는 10번 모두 똑같은 지점에 떨어질까? 아니다. 거기에는 바람과 같은 우리가 통제할 수 없는 변수들이 들어가 계속해서 결과는 달라질 것이다.
2. 변동성이란?
여기서 변동성이란 개념을 설명할 수 있다. 내가 수행할때마다 달라질 수 있는 성질을 의미하며, 대개 표본의 각 데이터 포인트 (X1, X2 등 각 포인트)마다 적용될 수 있다.

위의 그림으로 설명해보자. 각 데이터 포인트들을 샘플링 할때, 모든 포인트들은 모집단에서 랜덤 샘플링되기 때문에 (불확실성) X1이 3이 될수도, 5가 될수도, 10이 될수도 심지어 극단적으로 100000이 될 수도 있다. 즉, 위의 성질을 변동성이라 부른다.
3. 분산이란?
위의 불확실성 또는 변동성을 어떻게 수학적으로 표현 할 수 있는가를 따졌을때, 해당 집단을 대표하는 값인 기댓값을 기준으로 각 데이터가 떨어져 있는 정도를 계산해서 평균내는 방법이 있다. 이것이 분산의 개념이고 평균 거리의 개념이 된다.
분산을 왜 다음과 같은 수식으로 정의했을까?
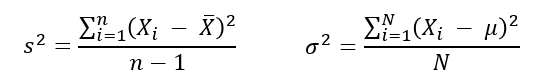

평균은 해당 집단을 대표하는 값, 즉 모든 값을 설명할 수 있는 값이라고 생각하면 된다. 하지만, 각 데이터들이 평균으로부터 멀리 떨어져 있을수록 평균의 설명력은 줄어든다. 즉 불확실성이 늘어 난다고 라고 할 수 있을 것이다.
위의 그림2에서 보면 (a)그림에서는 평균값이 X1부터 X5 근처에 있기때문에 평균으로 대부분의 값들을 설명할수 있지만, (b)의 경우에는 평균으로부터 떨어져 있는 거리가 멀어 평균자체로 각 데이털들을 설명하기에는 힘들어 보인다.
즉, (a)의 경우에는 표본의 대표로 평균을 사용해도 각 데이터의 불확실성이 낮아(평균으로 부터 튀는 정도) 무리가 없다. 반대로, (b)의 경우 어떤 데이터는 평균 근처에 있어서 괜찮을수도 있지만, 많은 데이터들이 불확실성이 높아(평균으로 부터 튀는 정도)가 높아 평균을 대표값으로 사용하기에는 무리가 있을수 있다.
불확실성을 평균으로부터 튀는 정도 = 평균으로부터의 거리 로 표현함으로써 정량화 할 수 있음을 알 수 있다. 분산이 높을수록 같은 수행을 했을때 튀는정도가 높아 평균과 동떨어진 어떤 엉뚱한 데이터가 튀어나올지 모른다.
위의 글을 다음과 같이 요약할 수 있다.
불확실성
- 우리가 통제할 수 없는 변인 / 원인
변동성
- 우리가 통제할 수 없는 변인으로 인해(불확실성에 의해) 수행할때마다 결과가 달라지는 성질
분산
- 불확실성/변동성을 수학적으로 수치화한 통계량
참고 자료
1. 통계학 입문 - 자유아카데미 (전공서적)
2. 학교 수업 자료 - 자료분석개론
3. 나의 정리된 생각 및 글 정리



